onEbest viewed with NetSurf
Numbers; logical and arithmetic operations Numbers
Although humans and many other animals have a natural ability to distinguish between groups with different numbers of objects, the symbolic representation of numbers is an invention which was developed within human civilisation
.
when University of Miami associate professor Caleb Everett and other anthropologists
worked with the indigenous Amazonian people known as the Pirahã, they realized the members of the tribe had
no word used consistently to identify any quantity, not even one.
Intrigued, the researchers developed further tests for the Pirahã adults, who were all mentally and
biologically healthy. The anthropologists lined up a row of batteries on a table and asked the Pirahã
participants to place the same number in a parallel row on the other side. When one, two or three batteries
were presented, the task was accomplished without any difficulty. But as soon as the initial line included
four or more batteries, the Pirahã began to make mistakes. As the number of batteries in the line increased,
so did their errors.
The researchers realized something extraordinary: the Pirahã’s lack of numbers meant they couldn’t
distinguish exactly between quantities above three.
The specialized form of knowing needed for literacy and numeracy skills is called symbolic representation. This develops gradually and is not evident until children are about 6 years old.
The most efficient system developed so far for representing numbers uses digits and number bases. In a base, a number is represented as a string of symbols called digits, like 123. The base, which is named according to the number of distinct symbols (digits) used, can also be specified: 12310. Base 2, which uses 2 symbols, 0 and 1, is currently used in most computers, but ENIAC and Charles Babbage's
Analytical Engine
, for instance, used
base 10. Example:12310 = 1·102+2·101+3·100 =
= 1·26+1·25+1·24+1·23+0·22+1·21+1·20 = 11110112
Elements of formal logic
Formal logic is the science of deductively valid arguments
.
An argument is a series of propositions in which one proposition, called the conclusion, is
presented as following from another set of propositions, called the premises. A proposition is a
statement which can be either true or false. All birds can fly, for instance, is a
false statement. The statement This statement is false, which refers only to itself, however, can
not be true nor false. This does not represent a problem, because the statement refers only to itself and
is thus never relevant in any situation, so there's no reason why anyone should think about
it.
An argument is deductively valid if and only if a false conclusion can not be obtained when all the premises are true. With a valid argument and at least one false premise, the conclusion can be false, but also true. The fundamental principle of logic says that if an argument is valid, then every argument with the same form is also valid, hence the term formal logic. True and false are considered truth values and are usually associated with numbers 1 and 0, respectively. Propositions or truth values can be connected by logical operators, some of which are shown in the following table, where A and B are the inputs and Q is the output:
| operator | symbol | logic gate representation | operation results | |
| not | ~ |  |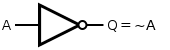
~0=1 | ~1=0 |
| and | & |  |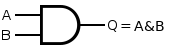
0&0=0 1&0=0 | 0&1=0 1&1=1 |
| or | | |  |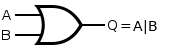
0|0=0 1|0=1 | 0|1=1 1|1=1 |
Other logic gates:
| name | logic gate representation | operation |
| buffer |  |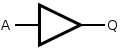
Q=A |
| nand |  |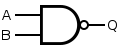
Q=~(A&B) |
| nor |  |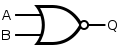
Q=~(A|B) |
| xor |  |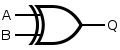
Q=(A|B)&(~(A&B)) |
| xnor |  |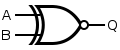
Q=~((A|B)&(~(A&B))) |
Arithmetic operations
The basic arithmetic operations which can be performed on numbers are addition, subtraction, multiplication and division. The simplest operation is adding two 1-bit positive numbers (in base 2), for which a device called half adder can be used. As can be seen below, it is composed of 2 logic gates: xor and and.
| half adder (HA) | |
|
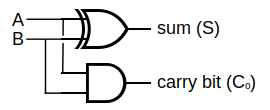
MD5: 7ced0ef2f6c80c954d325b0db66f792c
A and B are the input values and can be equal to 0 or 1. Storing the result requires 2 bits, because if A=B=1, then A+B=1+1=210=102, in which case Co=1 and S=0. Co is called carry bit because when n-bit numbers are added, this bit is carried to the next adder, which has to be a full adder with 3 inputs, as shown below.
| full adder (FA) |
|
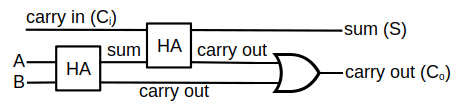
A full adder is composed of 2 half adders and an or gate. By connecting n full adders, an n-bit ripple carry adder can be formed, which can be used for adding two n-bit numbers, in which case the result will require n+1 bits for storage.
| 3-bit ripple carry adder |
|
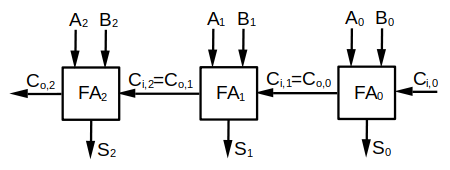
If, for instance, A=510=1012 and B=310=112, then the 3-bit adder above produces the following results:
| i | adder | Ai | Bi | Ci,i | Co,i | Si |
| 0 | FA0 | 1 | 1 | 0 | 1 | 0 |
| 1 | FA1 | 0 | 1 | 1 | 1 | 0 |
| 2 | FA2 | 1 | 0 | 1 | 1 | 0 |
The bits of the final result are Co,2=1, S2=0, S1=0 and S0=0, which means that:
A+B=510+310=1012+0112=10002=810
Larger numbers can be added by repeating the operation. For instance, 2 numbers composed of 6 bits can be added by first adding the rightmost (least significant) 3 bits and then the other 3, while considering Ci,0 equal to Co,2 from the previous operation.
For representing n-bit signed binary numbers, 3 methods can be used:
- signed magnitude: n-1 bits are used for the absolute value and the remaining 1 bit specifies the sign (0112=310, 1112=(-3)10);
- 1's complement: a negative number is represented by flipping (changing 1 to 0 and 0 to 1) all the bits of the corresponding positive number (0112=310, 1002=(-3)10);
- 2's complement: a negative number is represented by adding 1 to its 1's complement, i.e. flipping all the bits and adding 1 (0112=310, 1012=(-3)10).
310+(-3)10=0112+1012=10002
In base 2 the calculation looks the same as the previous one above (5+3), but this time the numbers are signed and after discarding the leftmost bit, the correct result, i.e. 0, is obtained.