onEbest viewed with NetSurf
Game with cannon Play
|
|
Download
The game was tested in Mozilla 1.4.1 from 2003 and should function in almost any browser that supports JavaScript.
MD5: 4767079b33cc8726b1b31224124f2d8b
Mathematical relations
If the position of the cannonball at time t is described by vector r(t) = (x(t) y(t))T, then the velocity v(t) and the acceleration a(t) are expressed by Equations (1) and (2):
dr(t)
v(t) = ----- (1)
dt
dv(t) d2r(t) F(t)
a(t) = ----- = ------ = ---- (2)
dt dt2 m
In this case, the force F depends on the velocity of the particle:F(v(t)) = G + R(v(t)); G = m·g R(v(t)) = -k·(v(t) - vw)·|v(t) - vw| (3)where g is the gravitational acceleration, G is the weight, R(v(t)) is the air's resistance (drag), v(t) is the speed of the particle and vw is the wind speed.
Equation of motion (2) can be solved numerically, which usually means finding r(t) and v(t) at t1, t2, t3,...,ti, ti+1,..., where ti+1 = ti + Δt. Some methods are exemplified below.
r(ti+1) = r(ti) + v(ti)·Δt v(ti+1) = v(ti) + a(ti)·Δt (4)Equations (4) are known as Euler's method and are used here.
r(ti+1) = r(ti) + v(ti)·Δt + a(ti)·(Δt)2/2 (5)Equation (5) is called the SUVAT method and is used in SimCar. The equations for the case in which the acceleration is considered to have a linear variation between ti and ti+1 can be found in file Equations.pdf from Cannon.zip, in my PhD thesis on pages 76 and 77, and in file doc/doc.pdf from mtfem-2.0.0.tar.gz, on pages 18 and 19. The methods presented so far are based on Taylor polynomials, but Verlet's method, suitable for computing trajectories of planets and other particles moving in various force fields, uses a slightly different approach (see Equations.pdf).
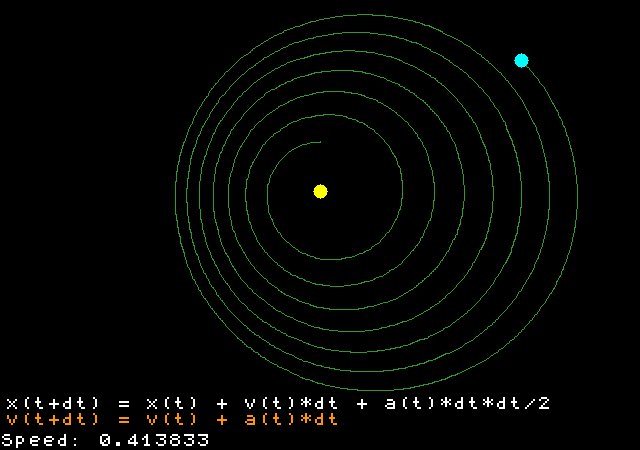Trajectory calculated with the SUVAT method
|
Trajectory calculated with Verlet's method (program included in
SDL_grf)
|
Ballista,
ZX Spectrum, 1983
|
ENIAC, a computer completed
in 1945 and designed to run similar games
|